Significado de «curva, matemática»

1. Toda línea continua que cambia constantemente de dirección se llama curva. La circunferencia, la parábola, la elipse, y la hipérbola son ejemplos de curvas simples. Pero en Matemáticas superiores aun la recta constituye una curva, pues se llama de este modo cualquier línea que representa una función analítica (v. Geometría analítica). En efecto, la longitud y trazado de muchas curvas, así como el área de la superficie que limitan, pueden determinarse mediante ecuaciones matemáticas y un sistema de ejes coordenados. Curvas tales como la cisoide y la cicloide, más complejas que las antedichas, tanto en lo referente a su construcción como a sus fórmulas, han sido determinadas analíticamente con exactitud (v. Cisoide; Cicloide). La cisoide fue empleada por Diocles de Alejandría en el año 100 a. de J.C. y Tolomeo, el año 200 d. de J.C., explicó el movimiento de los planetas tomando como base la cicloide.
   
   Como es evidente, una curva puede presentar las más variadas formas, tener un alto valor estético y ser por ello de aplicación práctica en las Bellas Artes; pero si no se logra definirla mediante una ecuación matemática adecuada, aquella curva carecerá de utilidad práctica en ciencias tales como la Física, la Ingeniería, la Economía, etcétera.
   
   Las curvas se emplean para explicar e ilustrar muchas leyes naturales. De ordinario, la trayectoria de, un proyectil es parabólica, tanto en el ascenso como en el descenso. La llamada curva exponencial pone de manifiesto, por ejemplo, cómo se produce la desintegración de un material radiactivo y por esto, mediante la ecuación de una curva exponencial apropiada, el científico puede predecir la cantidad de material radiactivo que quedará después de transcurrir cierto tiempo (v. Radiactividad). Los trabajos estadísticos se basan en la curva de distribución de frecuencias para resumir las características de grandes grupos de datos.
   
   Varias curvas simples pueden formar conjuntamente una curva más complicada. Así, en Música, las vibraciones de la nota fundamental corresponden a una curva simple (sinusoide; v. Trigonometría), pero cuando se trata de las ondas de un instrumento musical, las características de vibración del instrumento se superponen a la frecuencia fundamental y forman una curva compleja.
   
   Trazado de ima curva. Técnica para la representación gráfica de dos grupos de datos numéricos relacionados entre sí. La forma más elemental para la representación de una curva se hace sobre la base de pares de valores que se corresponden, .por ejemplo, los del volumen que adquiere un gas a diferentes presiones a que se le somete, datos que suelen aparecer en una tabla adecuada. Estos datos se trasladan a un sistema de coordenadas cartesianas, de modo que cada par de valores correspondientes definan un punto en el plano; uniendo luego todos estos puntos se obtiene una línea recta o curva, que responde a los valores correlativos que se trata de representar. Si no se dispone de tabla, el investigador se vale de ecuaciones que ligan entre sí a las variables y después de tabular una serie de valores correspondientes procede a la representación gráfica del modo anteriormente indicado.
   
   Sin embargo, a veces ocurre que la ecuación no puede convertirse fácilmente en una fórmula explícita sencilla y entonces se hace necesario recurrir a otros métodos para el trazado de la curva.
   
   Sea, por ejemplo, la curva representada por la función:
   
   y^2 = x^3 - 3x^2 + 2x
   
   
   
   
   
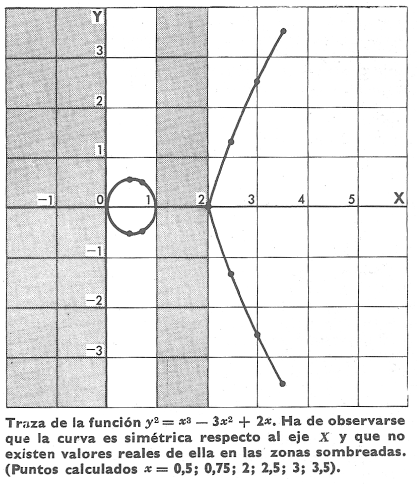
   Se estudian sucesivamente determinadas características que permiten reproducirla.
   
   1. Campo de variabilidad. Se observa que dando a x valores negativos, el segundo miembro es siempre negativo, en tanto que el primer miembro es siempre positivo; esta incompatibilidad evidencia que la función no puede estar representada entre los valores 0 y -∞. Una investigación más a fondo demuestra que tampoco está definida entre los valores 1 y 2 (zonas sombreadas de la figura).
   
   
   2. Simetría respecto a los ejes. Si la variable y se sustituye por (-y) el resultado no varía por ser y^2 = (-y)^2, lo que demuestra que la función toma idénticos valores tanto en el campo positivo como en el negativo de la variable; por lo tanto, la función es simétrica respecto al eje X. Análogamente, sustituyendo x por (.x) se obtiene la función
   
   
   y^2 = 3x^3 - 3x^2 - 2x,
   
   
   pero esta función es distinta de la primitiva, luego la función no es la misma para el campo positivo de la variable x que para el negativo; es decir, no es simétrica respecto al eje y: este extremo ha sido comprobado en el apartado 1.° al no estar definida la función en el campo negativo de x. Guando una curva es simétrica respecto a un eje, basta determinar los puntos situados a un lado del mismo y los del lado opuesto se obtienen por simetría.
   
   
   3. Intersección con los ejes. Para ver los puntos en que la curva cruza los ejes se hace sucesivamente y = 0 y x = 0. Para y = 0, x puede tomar los valores 0, 1 y 2, luego los puntos (0,0), (1,0) y (2,0) son puntos de la curva. Para x = 0, y toma solamente el valor 0, luego el punto (0,0) es el único situado sobre el eje «y»; como la función no está definida en el campo negativo se deduce que dicho eje «y» es tangente a la curva en dicho punto (0,0).
   
   
   4. Máximos y mínimos. Los puntos donde la curva alcanza sus valores máximos y mínimos se determinan en el cálculo diferencial igualando a cero la primera derivada de la función y sustituyendo los valores obtenidos de la ecuación resultante en la segunda derivada (v. Máximos y mínimos). En la función estudiada se presenta un máximo aproximadamente en el punto (0,42, +0,62) y un mínimo, deducido por simetría, en (0,42, -0,62).
   
   
   5. Crecimiento y decrecimiento. Estudiado el crecimiento y decrecimiento de la función en los intervalos en que está definida (0,1) y (2, ∞), mediante el valor positivo o negativo de la primera derivada, se comprueba que a partir del punto (2,0) la curva se extiende indefinidamente hacia +∞ y hacia -∞.
   
   
   Con los datos y puntos críticos conseguidos puede trazarse con gran aproximación la curva que se trata de representar. Otros criterios matemáticos proporcionan los puntos de inflexión eventuales, ramas asintóticas, etc., y el cálculo integral permite la determinación de las áreas relacionadas con la curva.
   
   
   Lo que importa ante todo es saber si la función es continua o no y en este último caso para qué valores se produce la discontinuidad.
   
   Curva de una función empírica. Método para hallar una fórmula o relación funcional (v. Función) que represente analíticamente una tabla de datos empíricos o estadísticos. El tipo de fórmula que mejor se adapta a los datos proporcionados por la tabla es su gráfica y se deduce del estudio de aquélla. Cuando los datos se representan en el diagrama y la gráfica que aparece es una línea recta puede comprobarse que las dos clases de datos, x e y, guardan la relación de una función de primer grado y = ax + b. La operación inmediata consiste en determinar los coeficientes a y b de tal modo qué sea mínima la diferencia entre los valores de y obtenidos por la fórmula y los valores que figuran en la tabla. Para determinar a y b se toma una serie de ecuaciones de la forma y = ax + b, dando a x e y los valores empíricos de la tabla. Las ecuaciones se dividen entonces en dos grupos, aproximadamente iguales, y se obtiene la ecuación promedio para cada una. Estas dos ecuaciones se resuelven entonces simultáneamente para los valores de a y b (v. Ecuación, Sistema de ecuaciones). Un procedimiento más exacto lo proporcionan las fórmulas deducidas del principio de que la suma de los cuadrados de las diferencias entre los datos calculados y los observados sea un mínimo. Véase MÍNIMOS CUADRADOS, MÉTODO DE LOS.
   
   
   Para relaciones menos simples entre las variables x e y, pueden admitirse otros tipos de curva (v. Curva). El Análisis matemático proporciona, además de los procedimientos arriba mencionados, otros métodos de cálculo. Una vez que ha sido elegida una fórmula adecuada para expresar los datos empíricos y determinados sus coeficientes, el investigador estudia esta función posteriormente mediante la aplicación de otras técnicas matemáticas. Véase Geometría analítica.

Compartir

Buscar

Asistente IA

Consulta nuestro asistente de Inteligencia Artificial
¡te responderá en segundos!

Respuesta completa
Respuesta corta

[ Ayuda ] Dale información suficiente de lo que buscas, dale un contexto. El Asistente te puede dar definiciones, sinónimos y antónimos, oraciones de uso de palabras, encontrar ideas relacionadas, corregir ortografía y darte asistencia escolar sobre cualquier tema. Igualmente, te recomiendo FUERTEMENTE que uses nuestro Buscador (más abajo) para encontrar información apropiada, ya que esta fue escrita por nuestros expertos.

* ACLARACIÓN: sugerimos dejar un email para que te contactemos si vemos errores en la respuesta de la IA: leemos todas las consultas.

Esta imagen puedes emplearla con fines didácticos en la escuela, institución educativa o proyectos web.

¿Hay un error o desea enviarnos un mensaje?: enviar mensaje

No hay ningún comentario todavía